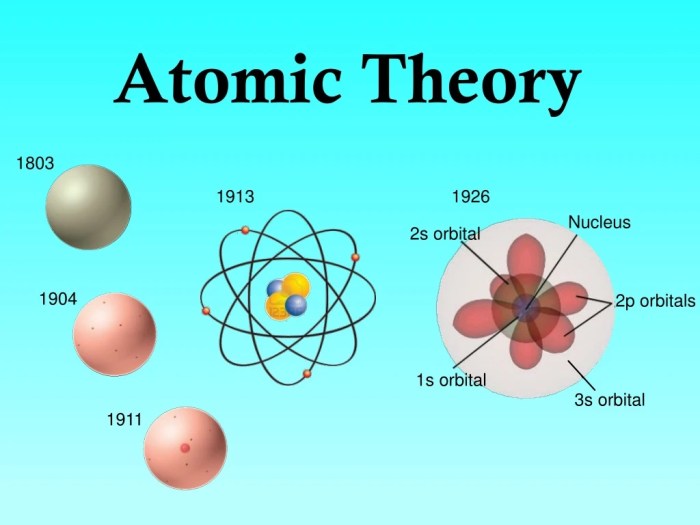
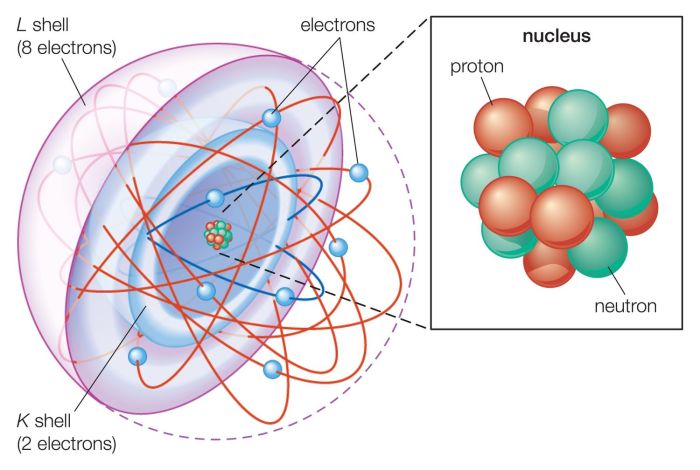
Magic square atomic structure and theory is a fascinating field that combines the ancient wisdom of magic squares with the cutting-edge science of atomic physics. This interdisciplinary approach has led to new insights into the fundamental nature of matter and the universe itself.
Magic squares are mathematical constructs that have been studied for centuries. They are arrangements of numbers in a square grid, such that the sum of the numbers in each row, column, and diagonal is the same. Magic squares have been used for a variety of purposes, from divination to cryptography.
Magic Square Theory: Magic Square Atomic Structure And Theory

Magic squares are arrangements of numbers, usually in a square grid, such that the numbers in each row, column, and diagonal add up to the same constant. Magic squares have been studied for centuries and have been found in many different cultures.
The mathematical properties of magic squares are well-understood. The sum of the numbers in any row, column, or diagonal is called the magic constant. The magic constant for a magic square of order n is given by (n^3 + n)/2.
Magic squares can also be constructed using a variety of methods, including the De La Loubère’s method and the Siamese method.
Magic Square and Atomic Structure, Magic square atomic structure and theory
Magic squares have been used to model atomic structures since the early 20th century. The first person to use magic squares in this way was the physicist Niels Bohr. Bohr used a magic square to model the structure of the atom, and he found that the magic constant was equal to the atomic number of the element.
This led to the development of the nuclear shell model, which is still used today to understand the structure of atoms.
Magic squares have also been used to model the electronic structure of atoms. The electronic structure of an atom is determined by the number of electrons in each energy level. Magic squares can be used to represent the energy levels of an atom, and the magic constant is equal to the number of electrons in each energy level.
Historical Context
The earliest known magic squares were found in China during the Han Dynasty (206 BC – 220 AD). These magic squares were used for divination and were believed to have magical powers. Magic squares were also used in India and the Middle East during the Middle Ages.
In the 16th century, magic squares were introduced to Europe, and they quickly became popular among mathematicians and scholars.
Magic squares have been studied by many famous mathematicians, including Leonhard Euler, Carl Friedrich Gauss, and Srinivasa Ramanujan. These mathematicians have made significant contributions to the theory of magic squares, and they have helped to develop new methods for constructing and analyzing magic squares.
Applications of Magic Squares
Magic squares have a wide variety of applications beyond atomic structure. They are used in mathematics, computer science, and architecture. In mathematics, magic squares are used to study number theory and combinatorics. In computer science, magic squares are used to design error-correcting codes and to solve optimization problems.
In architecture, magic squares are used to design buildings and landscapes.
| Field | Application |
|---|---|
| Mathematics | Number theory, combinatorics |
| Computer science | Error-correcting codes, optimization problems |
| Architecture | Building design, landscape design |
Design and Construction of Magic Squares
There are a variety of methods for designing and constructing magic squares. One of the most common methods is the De La Loubère’s method. This method starts with a magic square of order 3 and then uses a series of transformations to create magic squares of higher order.
Another common method is the Siamese method. This method starts with a magic square of order 4 and then uses a series of transformations to create magic squares of higher order.
There are also a number of software programs that can be used to generate magic squares. These programs can be used to generate magic squares of any order, and they can also be used to analyze the properties of magic squares.
Cultural Significance of Magic Squares
Magic squares have been used in a variety of cultures throughout history. In China, magic squares were used for divination and were believed to have magical powers. In India, magic squares were used in religious ceremonies and were believed to bring good luck.
In the Middle East, magic squares were used in architecture and were believed to protect buildings from evil spirits.
Magic squares continue to be used in a variety of cultures today. They are used in art, literature, and religion. Magic squares are also used in education, and they can be used to teach children about mathematics and problem-solving.
Open Questions and Future Research
There are a number of open questions and areas for future research in magic squares. One area of research is the development of new methods for constructing magic squares. Another area of research is the study of the properties of magic squares.
Researchers are also interested in exploring the applications of magic squares in other fields, such as quantum computing and artificial intelligence.
Magic squares are a fascinating and versatile mathematical object. They have a long history and have been used in a variety of cultures. Magic squares continue to be a source of inspiration for mathematicians and scientists today, and they are likely to continue to be studied for many years to come.
FAQ Section
What is a magic square?
A magic square is a square grid of numbers such that the sum of the numbers in each row, column, and diagonal is the same.
How are magic squares used in atomic structure theory?
Magic squares can be used to model the electronic structure of atoms. This can lead to new insights into the nature of chemical bonding and the properties of materials.
What is the future of magic square atomic structure and theory?
The field of magic square atomic structure and theory is still in its early stages, but it has the potential to revolutionize our understanding of the fundamental nature of matter. As we continue to explore this fascinating field, we can expect to uncover even more amazing secrets about the universe.